Digging into Divergence Loss

Understanding the risks of being an AMM liquidity provider for x*y=k type pools. (First published 02 Dec 2020)

Introduction

As a liquidity provider on Uniswap, I’m exposed to divergence loss. This is a measure of the impact that changing prices has on my liquidity Pool (LP) tokens compared to holding the tokens in a cold wallet. This due to the automated money maker (AMM) acting to sell the token that increases in value compared to the other token. Trading fees (typically 0.3% of each trade), and liquidity mining rewards used to encourage liquidity can both offset the impact of the losses and so encourage the provision of liquidity.

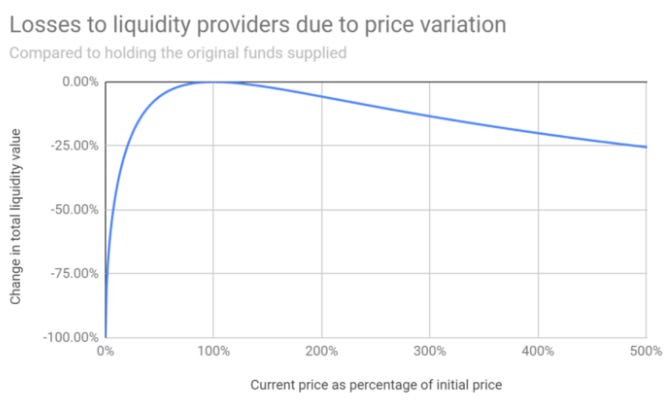
Pintail has published a couple of articles covering the returns from Uniswap pools. With the oft shared Figure 1. From this it’s clear that as the prices diverge, there is a loss. However, while this makes sense to me, I felt like I didn’t have sufficient understanding of what was going on.

Figure 1: https://pintail.medium.com/uniswap-a-good-deal-for-liquidity-providers-104c0b6816f2

Note, the initial articles referred to Impermanent loss (IL) as the change in price ratios may not be permanent. However, this loss would be crystalised if you leave the LP. I, like many others, prefer to use the term Divergence Loss, as it better reflects the link between price divergence and loss to the LP.

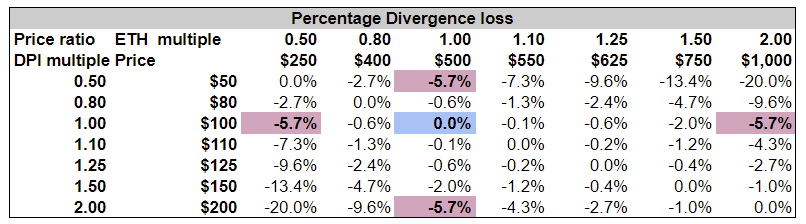
As an example, if one of the tokens increased by a factor of 2, then there is a 5.7% divergence loss compared to just holding the tokens outside the LP.

Figure 2: CoinGecko divergence loss calculator

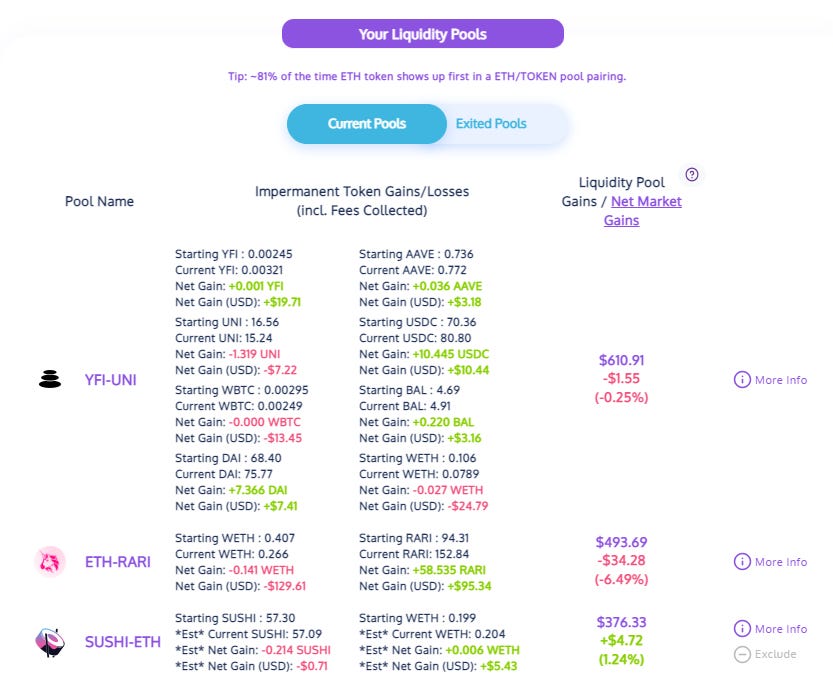
There are some excellent tools to help the LP understand how the pool has performed that includes the impact of divergence loss and trading fees (e.g. Apy.vision in figure 3 looking at a random wallet). Note that many do not include farming income.

Figure 3:apy.vision report for a random liquidity pool showing impact of divergence loss and trading fees

This blog is really my attempt to understand the maths behind divergence loss.

Divergence Loss — A worked example

I’m going to look at the DPI:ETH pair and assume a starting price of $500 and $100 with a total investment of $1,000.

Table 1: Starting portfolio and price ratios

Then I’m going to look at the effect as the price of each increased or decreases using multiples of the initial price 0.5, 0.8, 1.0 ,1.1, 1.25, 1.5, 1.75 and 2.0. i.e either token can drop by 50% or grow by 100% from the initial values. The key consideration is the ratio between the prices. If there is no change in this ratio, then there is no divergence loss.

Table 2: Price ratios (5 is the starting ratio)

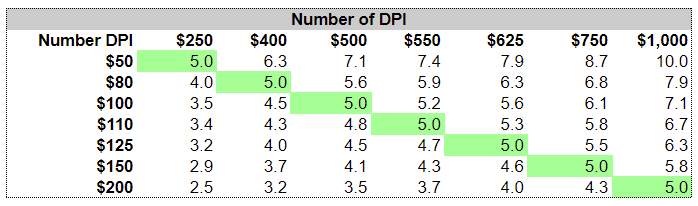
When the price ratio changes, the number of ETH (presented by the same LP token) can be calculated by the following equation (Table 2):

#ETH tokens = Square root ( pool K / Price ratio)

Table 3: Calculated number of ETH in LP for different price combinations

As the pool K is constant the number of DPI can be calculated (Table 3):

#DPI tokens = Pool K / # ETH Tokens

As we now know the price and number of each token in the liquidity pool for any combination of tokens we can calculate the:

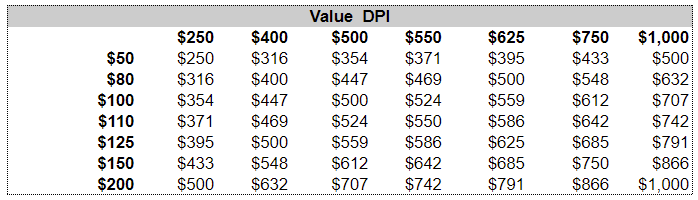
• Value of ETH (Table 5)

• Value of DPI (Table 6)

• Value of the pool (Table 7)

Table 5: Total value of ETH in LP for different price combinations

Table 6: Total value of DPIin LP for different price combinations

Table 7: Total value of LP for different price combinations

Then it’s a case of calculating the value of the tokens if we had held them outside the liquidity pool (= initial number * new price).

Table 8: Hold value of portfolio if tokens had not been in LP

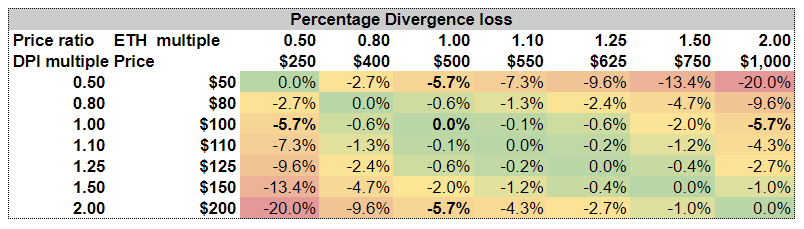
By subtracting the hold value from the LP value, we can calculate the divergence loss in $USD and Percentage.

Table 9: Divergence loss (LP value — hold value) for different prices

Table 10: Percentage divergence loss (LP value — hold value) for different prices

One key feature is that divergence is totally symmetrical. So if either token changes by a factor of 2 vs the other then there is a 5.7% divergence loss. This is independent on the token, or the direction of the divergence.

Table 11: Symmetry of percentage divergence loss (starting from $500 ETH and $100 DPI)

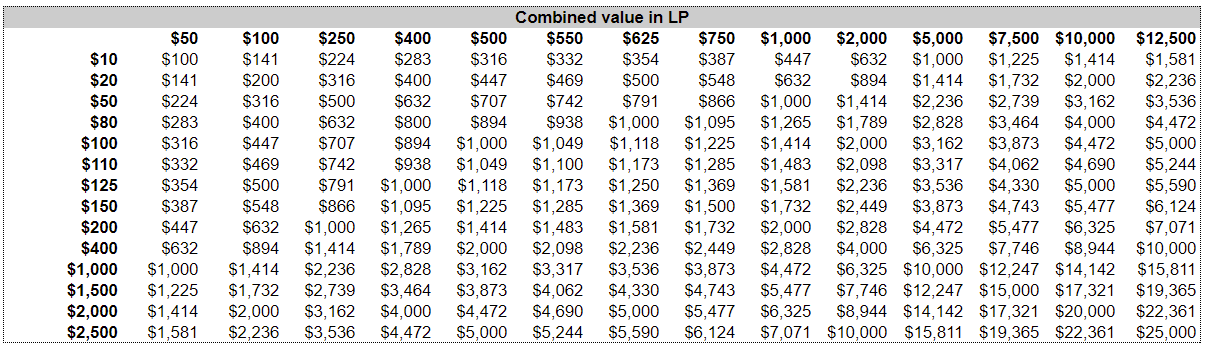
Obviously this can be scaled up to look at larger values and larger changes:

Table 12: LP value with larger changes in token prices (Starting $1,000 invested at $500 ETH and $100 DPI)

Table 13: Percentage divergence loss for larger price movements.

Final Thoughts

I think this exercise has been useful in helping me understand the risks I’m facing as a LP.

As a final bonus, I’ll provide a link to my spreadsheet for you to copy and a try inputting different values. Enjoy.

Disclosure and Disclaimer

I’m a long term investor in crypto currencies including DeFi. I am an active member of the INDEXcoop which manages the $DPI fund.

This is not financial advice, all investments are risky, crypto investments are more risky than most. Do your own research. Do not invest more than you can afford to lose.

@over-analyser on twitter